
I
nterpretation eines Gamma-Spektrums am Beispiel von Cs-137
Beim Zerfall des radioaktiven Isotops Cs-137 ist die Aussendung von Gamma-Quanten der Energie W = 662 keV
charakteristisch. (Dabei geht zunächst der Cs-137 Kern unter Aussendung von Beta-Strahlung in den angeregten Ba-137 Kern
über, welcher sich durch Abgabe dieser 662 keV Quanten stabilisiert.)
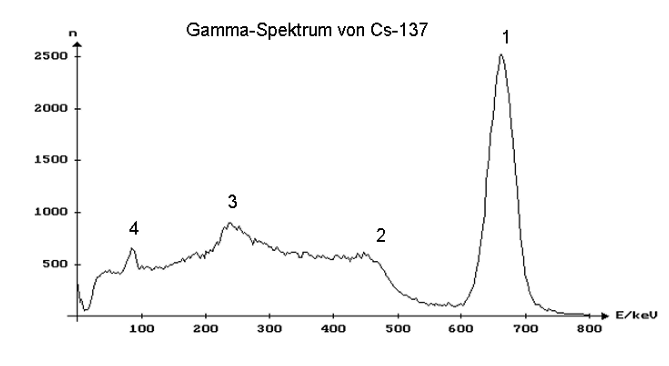
Spektroskopiert man nun ein Cs-137 Präparat mit einem schulüblichen Szintillationszähler, so erhält man aber keineswegs nur
einen monoenergetischen Peak bei 662 keV. Die Abb. zeigt, dass im niederenergetischen Bereich weitere Ereignisse registriert
werden.
Um dieses Energiespektrum prinzipiell zu verstehen, sollte man sich zunächst vor Augen führen, daß die Energieaufnahme im
Szintillationskristall bei allen Quantenprozessen durch die Vermittlung von Elektronen im Kristall erfolgt. Es sind hierbei drei
unterschiedliche Prozesse zu betrachten:
Siehe Nummerierung in der Darstellung des Spektrums.
1:
Die Gesamtabsorptionslinie (Photopeak)
Das hohe, relativ monoenergetische Hauptmaximum wird Photopeak oder auch Gesamtabsorptionslinie genannt. Dabei wird
die gesamte Energie des 662 keV Photons vollständig durch Photoeffekt an den Kristall abgegeben. Dabei "verschwindet" das
Lichtquant und die Energie des Photoelektrons wird im SEV (Sekundär-Elektronen-Vervielfacher) verstärkt und schließlich als
Zählimpuls demjenigen Kanal zugeordnet, der der Energie von 662 keV entspricht.
2: Die Compton-Kante
Die über einen breiten Energiebereich verteilten Ereignisse im niederenergetischen Teil des Spektrums nennt man Compton-
Kontinuum, ihre Abgrenzung zum höherenergetischen Teil heißt Compton-Kante. Für ihre Entstehung sind Compton-Ereignisse
im Zählerkristall verantwortlich:
Die 662 keV - Quanten treffen im Kristall auf "quasi-freie" Elektronen und geben an diese einen Teil ihrer Energie ab, wobei der
Energiebetrag nach Compton vom Streuwinkel abhängt.
Der maximale Energiebetrag, den ein Compton-Elektron auf diese Weise aufnehmen kann, berechnet sich nach folgender
Formel, wenn für a = 180 eingesetzt wird (Compton-Rückstreuung):
Beziehungsweise entspechended Werte eingesetzt:
3: Die Rückstreulinie
Da Compton-Streuprozesse im Kristall in allen Winkelbereichen von 0 Grad bis 180 Grad auftreten, werden Compton-
Elektronen mit Energiebeträgen von 0 keV bis 478 keV registriert und den entsprechenden Kanälen zugeordnet. Während für
die beiden bisher beschriebenen Teile des Spektrums Ereignisse im Zählerkristall verantwortlich sind, muss die Ursache für die
Entstehung der Rückstreulinie außerhalb des Szintillationszählers gesucht werden:
Gewöhnlich verwendet man radioaktive Präparate, welche in einer Halterung des Strahlerstiftes eingebettet sind. Die Gamma-
aktive Substanz strahlt darin zunächst nach allen Seiten, wobei es vorkommt, dass hf = 662 keV - Quanten, welche in die dem
Zähler entgegengesetzte Richtung gestrahlt werden, bereits in der Präparateumgebung Compton-Streuungen erfahren und
schließlich als Streuquanten der Energie hf vom Szintillationszähler registriert werden.
Nun kann zunächst vereinfachend angenommen werden, dass außerhalb des Zählerkristalls alle Streuwinkel
gleichwahrscheinlich sind. Betrachtet man aber den Zusammenhang zwischen dem Streuwinkel und dem Energie des
gestreuten Quants hf, so stellt man folgenden funktionalen Zusammenhang fest:
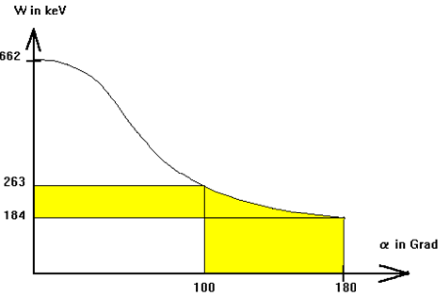
wobei der Graph der Zuordnung folgendermaßen aussieht:
Man sieht, dass alle Energiequanten hf, welche im
Winkelbereich zwischen 100
o
und 180
o
gestreut werden, einem
eng begrenzten Energiebereich zugeordnet werden. Diese
Quanten werden mittels Photoeffekt im Szintillationskristall
registriert (als unterschiedliche Gesamtabsorptionslinien in
diesem Bereich). Eine Überhöhung der Zählrate in den
entsprechenden Kanälen ist die Folge, wobei ein nicht sonderlich
scharf ausgeprägtes Maximum zustandekommt.
Made with MAGIX

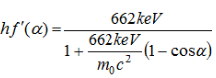
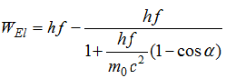
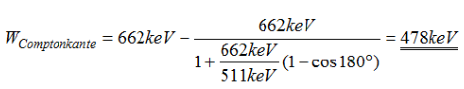
4: Die K-Linie von Blei
Da bei der Aufnahme des Spektrums eine Bleiabschirmun
g verwendet wurde, ist im
niederenergetischen Bereich zusätzlich die Röntgenfluoreszenzlinie von Blei zu sehen. Da hier
die K-Alpha und die K-Beta Linie nicht aufgelöst werden, kann man von einer mittleren Röntgen K-
Energie ausgehen, die nach Moseley (siehe: Moseley-Gesetz) für Blei (Z=82)
bei 77 keV liegt.
Gamma-Spektren weiterer Elemente:
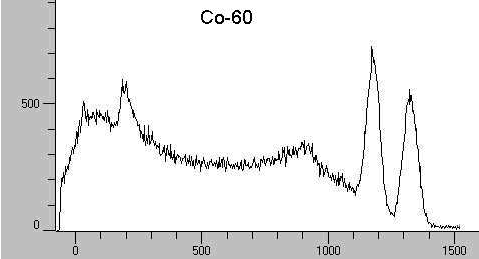
Cobalt-60
Co-60 hat zwei Photopeaks, deshalb überlagern sich die daraus resultierenden Compton-Ereignisse
zu einem überhöhten Compton-Kontinuum.
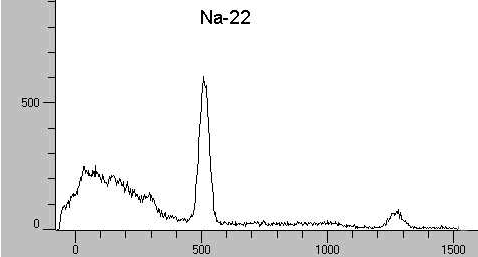
Natrium-22
Aufgrund seiner geringen Halbwertszeit von 2,6 a ist Na-22 als Schulpräparat problematisch.
Allerdings ist die Paarvernichtungsstrahlung wohl eine einzigartige Möglichkeit, die Einsteinsche Gleichung E = m c
2
meßtechnisch zu erfahren:
Dieser interessante Aspekt ergibt sich bei der genaueren Analyse des Gamma-Spektrums von Na-22. Zunächst
erhält man bei korrekter Einstellung der Hochspannung und Eichung der Energie-Achse zwei deutliche Peaks
bei ca. 1275 keV und 511 keV.
Zieht man zur Orientierung das Zerfallsschema von Na-22 zu Rate, so stellt man fest, dass Na-22 unter Aussendung
eines Positrons zu Ne-22 zerfällt. Dieses Neon-Isotop ist zunächst hochangeregt und gibt seine Energie in Form
eines Gamma-Quants mit der Energie von 1275 keV ab. Ein weiterer Übergang ist nicht dokumentiert.
.
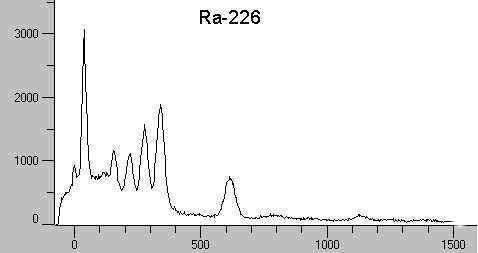
Radium-226
Radium hat ein sehr komplexes
g-Spektrum. Jedoch ist eine korrekte Zuordnung der Peaks zu den
"gamma-aktiven" Zerfallsprodukten von Ra-226 durchaus möglich.
Sehr interessant ist auch das Studium verwandter Spektren wie das von Radon (siehe: Radon-Analyse) und
natürlichen Uranerzproben.
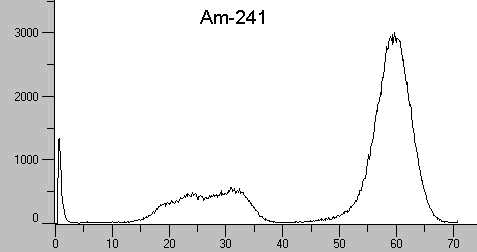
Americium-232
Am-241 hat unter den dargestellten Spektren die geringste
-Energie von 59,5 keV ( aus
g-Übergang zu Np-237). Das
"Energiegebirge" im niederenergetischen Bereich ist kein Compton-Kontinuum. Die zu erwartende Compton-Kante wäre bei 11 keV
(hier nicht darstellbar). Die Energien in diesem Bereich stammen aus L-Strahlung von Np, sowie von der K-Anregung von Jod (im
Zähler).
Thorium-232

Es ist also zu klären, weshalb im Bereich von 511 keV ein derart ausgeprägter Peak auftritt.Die Lösung liegt darin
begründet, dass Na-22 ein Beta+ Strahler ist. Die Positronen reagieren beim Zerfall sofort mit Elektronen unter Aussendung von
Vernichtungsstrahlung.
Dieser experimentelle Befund ist ein schönes Beispiel, um die Einsteinsche Masse-Energie-Äquivalenz zu zeigen:
m
e+
c
2
+ m
e-
c
2
= 2 Eg (Gammaenergie)
Wegen des Impulserhaltungssatzes bilden sich beim Vernichtungsprozeß zwei Gamma-Quanten der Energie Eg = 511 keV,
welche in entgegengesetzte Richtungen wegfliegen. Eins dieser Quanten wird vom Szintillationszähler registriert.
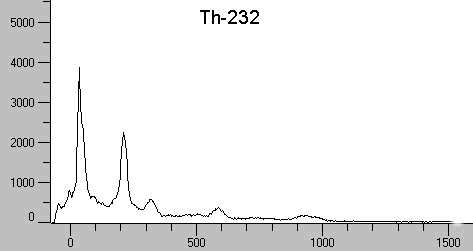
Ähnlich wie beim Radium-Spektrum ist auch hier der "Fingerabdruck" einiger Zerfallsprodukte von Thorium zu sehen, soweit die
Tochternuklide durch Abgabe von
g-Quanten in den Grundzustand übergehen.
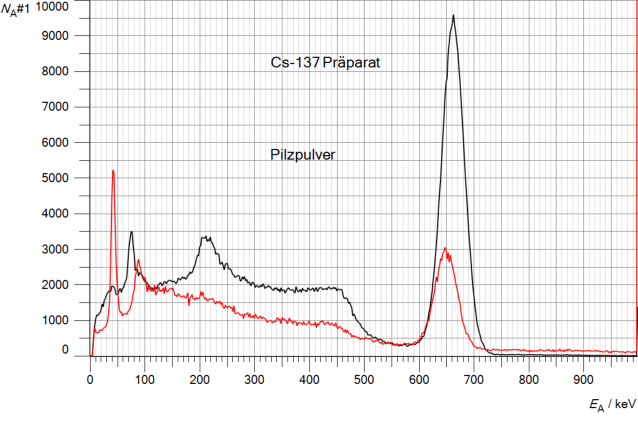
Die rote Kurve im Spektrum zeigt die Analyse von Steinpilzpulver, welches im Jahr nach dem Tschernobyl-Reaktor-Unfall in einem
polnischen Lebensmittelladen gekauft wurde. Selbst ohne Subtraktion des Nulleffektes und mit einer relativ geringen
Messdauer von etwa 5 Minuten erkennt man die erhebliche Kontamination mit Cs137, welche durch das Vergleichsspektrum mit
einem Cs-Schulpräparat (schwarze Kurve) bestätigt wird.
Norbert Großberger 2015

Nachwirkungen von Tschernobyl
















